
Workshop on Numerical Weather Models for Space Geodesy Positioning
24-25 October, 2011
Room C25 (ADI Room), Head Hall Building
Support:
Atlantic Association for Research in the Mathematical Science

International Association of Geodesy
Program
October 24 – Monday
- 9:00 – Opening and Welcome
- 9:20 – The troposphere: the problem, its modelling and its mapping
- 10:00 – Measurements, Water Vapour Radiometer, and applications
- 10:20 – Coffee break
- 10:40 – GEM Numerical Weather Models
- 11:05 – A snapshot of UNB Ray-tracer
- 11:30 – UNB-VMF1: motivation, status and future
- Lunch (on your own)
- 13:30 onwards – discussions on ray-tracing and UNB-VMF1
October 25 – Tuesday
- 9:00 onwards – discussions on ray-tracing and UNB-VMF1
- Lunch (on your own)
- 13:30 onwards – final gathering, conclusions and plans for the future
Workshop motivation, description and objectives
Signals transmitted from global navigation system satellites, such as those of the US Global Positioning System (GPS) cross the Earth's atmosphere and suffer from refraction, causing the measured distance to be biased (delayed). One of the layers of the atmosphere crossed by the signals is the neutral atmosphere, which includes the troposphere, where meteorological phenomena happen. The delay suffered by the signal is a function of meteorological parameters, such as pressure, temperature and humidity. A way to deal with this neutral-atmosphere delay has been to use models based on climatology. In the past decade, the use of numerical weather models (NWM), the same ones used for weather forecasts, started to be investigated for modelling the neutral-atmosphere delay. The advantage of using NWM is that it provides the best available representation of the neutral atmosphere at any given time. The disadvantage is that its use is computationally demanding, notably for real-time applications.
At UNB, we have been investigating the use of NWM for space geodesy positioning and applications since 2004, and collaborating with research groups around the world. We have developed a ray-tracer to ray-trace through NWM and we have been developing a service to provide ray-traced neutral-atmosphere delays to be used in GNSS positioning. This service will run under the auspices of the International Association of Geodesy. We have developed capabilities to use the Canadian Meteorological Center GEM Model, as well as the National Oceoanographic and Atmospheric Administration (NOAA) NCEP model and the European Center for Medium-range Weather Forecasting (ECMWF) model.
The workshop will gather together a few specialists dealing with numerical weather models, assimilation, modelling, ray-tracing, and slant factor compression, focusing on geodetic positioning, including scientists from Environment Canada and the University Corporation for Atmospheric Research (UCAR). Students are encouraged to participate.
Background
Traditionally, the delay suffered by electromagnetic waves when crossing the neutral atmosphere (the portion of the atmosphere composed primarily of the troposphere and the stratosphere) has been modelled by tropospheric models (that provide the delay at the zenith) and mapping functions (that map the delay for the elevation angle of the satellite) based on climatological information, e.g., Hopfield [1969], Saastamoinen [1972], Niell [1996], Leandro et al. [2008]. In the past decade, numerical weather models (NWM) have been investigated as an alternative for extracting the delay directly, through ray-tracing, or to improve mapping functions [Niell, 2003; Boehm et al., 2006a; Boehm et al., 2006b].
Extraction of the neutral-atmosphere delay from NWM involves a process of ray-tracing [Nievinski, 2010] through a particular NWM. There are several different ways of doing that, depending on the refractive index formula adopted (e.g., Essen and Frome [1951], Thayer [1974], Bevis et al. [1994], Rüeger [2002]), on the assumption of the atmospheric structure (whether tangent plane, spherical concentric, spherical osculating, spherical normal, ellipsoidal, gradient, or 3D free-form), ray-path model (zenith, straight-line, bent-2D or bent-3D), and on the integration process used. There is no single or consensual way of ray-tracing through the neutral atmosphere, as illustrated in Nafisi et al.[2011], paper that compares different implementations of ray-tracing by several institutions (UNB, TUV, GFZ, NIICT, CRGS). Other potential sources of discrepancies lie with the fact that the various NWM models available have a few differences among them (e.g., the European Centre for Medium-Range Weather Forecasts⎯ECMWF, NOAA's National Center for Environmental Prediction⎯NCEP, the Canadian Environmental Multiscale⎯GEM).
The process of deriving the neutral atmosphere delays directly from NWM is time-consuming and computationally expensive, and imposes logistical constraints for use especially in real-time positioning applications. Therefore, there has been an effort to develop mapping functions based on the more realistic NWMs. Such is the case of the Isobaric Mapping Function (IMF), the Vienna Mapping Functions 1 (VMF1) and the Global Mapping Function (GMF). In essence, they all follow the continued fraction form suggested by Marini [1972] for the hydrostatic and wet mapping functions for an elevation angle e:
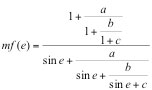
Three coefficients a, b and c are sufficient to map zenith delays down to elevations angles of 3°. In the case of IMF and the VMF1, these coefficients are determined from ray-tracing through NWM. The GMF is determined from a spherical harmonics fit to the VMF1.
The VMF1 have been generated on a daily basis in grid format as a service of the International Association of Geodesy, under the Global Geodetic Observing System (GGOS) project. They are generated by the group at the University of Vienna using data from the ECMWF. At UNB, we have developed capabilities to generate VMF1 (referred as the UNB-VMF1) using data either from the GEM or from the NCEP models. The UNB-VMF1 have been generated on a test-basis and it will be generated as an additional IAG service, as an alternative and backup to the VMF1 currently generated. Since the UNB-VMF1 uses a different ray-tracing algorithm and a different NWM they will provide additional data for scientific investigations.
Mathematical aspects to be discussed during the gathering are related to: (a) The status of the GEM and NCEP models including assimilation of data into the model and its dissemination. A key aspect in geodetic and geophysical applications is to have “error bars” for all parameters. Currently, NWMs do not provide them. Should this information be added at the assimilation? Can model verifications be used for that purpose? Would it be possible then to provide error bars for ray-tracing products (such as the UNB-VMF1)? (b) Modelling is based on an assumption of hydrostatic equilibrium. Can we put an error bound on this assumption (using radiosondes equipped with both barometer and GPS)? (c) Should refractivity coefficient values used in ray-tracing be refined? (d) How efficient would a slant factor compression be for the dissemination of ray-traced parameters? (e) Geodetic positioning. How much do tropospheric parameters (zenith delays and gradients) act as “fudge factors” for other error sources, e.g., antenna phase-center (APC), atmospheric pressure loading (APL), and sub-daily station displacements?
References
- Bevis, M., S. Chiswell, S. Businger, T. A. Herring, and Y. Bock (1996).
- “Estimating wet delays using numerical weather analyses and predictions.”Radio Science, Vol. 31, No. 3, pp. 477–487, doi:10.1029/96RS00008.
- Boehm, J., B. Werl, and H. Schuh (2006a).
- “Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data.” Journal of Geophysical Research, Vol. 111, No. B02406, doi:10.1029/2005JB003629.
- Boehm, J., A. E. Niell, P. Tregoning, and H. Schuh (2006b).
- “Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data.” Geophysical Research Letters, Vol. 33, No. L07304, doi:10.1029/2005GL025546.
- Essen, L., and K. D. Froome (1951).
- “The refractive indices and dielectric constants of air and its principal constituents at 24,000 Mc/s.” Proceedings of the Physical Society, Section B, Vol. 64, pp. 862–875, doi:10.1088/0370-1301/64/10/303.
- Hopfield, H. S. (1969).
- “Two-quartic tropospheric refractivity profile for correcting satellite data.” Journal of Geophysical Research, Vol. 74, No. 18, pp. 4487–4499.
- Leandro, R. F., R. B. Langley, and M. C. Santos (2008).
- “UNB3m pack: a neutral atmosphere delay package for radiometric space techniques.” GPS Solutions, Vol. 12, No. 1, pp. 65–70, doi:10.1007/s10291-007-0077-5.
- Marini, J. W. (1972).
- “Correction of satellite tracking data for an arbitrary tropospheric profile.” Radio Science, Vol. 7, No. 2, pp. 223–231, doi:10.1029/RS007i002p00223.
- Nafisi, V., L. Urquhart, M. C. Santos, F. G. Nievinski, J. Böhm, D. D. Wijaya, H. Schuh, A. A. Ardalan,T. Hobiger, R. Ichikawa, F. Zus, J. Wickert, P. Gegout (2011).
- Benchmarking ray-traced tropospheric delays. Accepted for publication in IEEE Trans. on Geoscience and Remote Sensing.
- Niell, A. E. (1996).
- “Global mapping functions for the atmosphere delay at radio wavelengths.” Journal of Geophysical Research, Vol. 101, No. B2, pp. 3227–3246, doi:10.1029/95JB03048.
- Niell, A. E. (2003).
- “The IMF mapping functions.” International Workshop on GPS Meteorology, Tsukuba, Japan, January 14–17.
- Nievinski, F. G. (2009).
- Ray-tracing Options to Mitigate the Neutral Atmosphere Delay in GPS. M.Sc.E. thesis, Department of Geodesy and Geomatics Engineering Technical Report No. 262, University of New Brunswick, Fredericton, New Brunswick, Canada, 232 pp.
- Rüeger, J. M. (2002).
- “Refractive index formulae for radio waves.” FIG XXII International Congress, International Federation of Surveyors (FIG), Washington, D.C., April 19–26.
- Saastamoinen, J. (1972).
- “Atmospheric correction for the troposphere and stratosphere in radio ranging of satellites.” In The Use of Artificial Satellites for Geodesy, eds. S. W. Henriksen, A. Mancini, and B. H. Chovitz, Vol. 15 of Geophysical Monograph Series, American Geophysical Union, Washington, D.C., ISBN 0-87590-015-1, pp. 247–251.
- Thayer,G.D. (1974).
- “An improved equation for the radio refractive index of air.” Radio Science,Vol.9, No.10, pp.803–807, doi:10.1029/RS009i010p00803.

